Cette annexe au tutorial C va nous permettre de voir, brièvement,
ce que sont les bases numériques, et, surtout, comment convertir
des nombres d'une base à une autre.
Ces explications n'ont pas été intégrées directement
au Chapitre 6 du tutorial, auquel elles se rattachent, afin de ne
pas l'alourdir avec des informations qui n'entrent pas vraiment dans le
cadre de son sujet.
I:\ Quelques notions de Bases, vraiment indispensables
En général, on désigne sous le terme de "Base
n" la base qui utilise les chiffres de 0 à n-1. Par exemple,
nous utilisons quotidiennement la base 10, aussi appelée décimale,
qui utilise les chiffres de 0 à 9.
Le Compilateur GCC, et donc, TIGCC, est capable de "comprendre"
les bases 2 (binaire), 10 (décimal), et 16 (hexadécimal).
La base 10 est reconnue car c'est elle que nous avons l'habitude de manipuler,
la base 2 est admise car c'est la plus proche de la machine (chaque bit
peut prendre deux valeurs : 0 ou 1, le courant passe ou ne passe pas,
la charge magnétique est positive ou négative, ...), et
la base 16 est employée pour minimiser le nombre d'erreurs à
la lecture et à l'écriture par rapport à la base
2 (car 4 chiffres binaires correspondent à un chiffre hexadécimal).
En langage C, les nombres exprimés en base 2 doivent être préfixés par "0b" (le chiffre zéro et la lettre B, en minuscule), les nombres exprimés en base 16 doivent être préfixés par "0x" ou "0X" (le chiffre zéro, et la lettre X, en minuscule ou majuscule), et les nombres en base 10 ne doivent pas être préfixés.
En base 16, puisque notre alphabet ne comporte pas 16 chiffres, nous
utilisons les dix chiffres usuels, soit de 0 à 9, puis les six
premières lettres, soit de A à F.
A présent, nous désignerons sous le terme de "digit"
chaque chiffre d'une écriture (il s'agit du terme anglais pour
"chiffre") ; cela parce que le terme de "chiffre"
n'est pas adapté aux écritures hexadécimale, qui
peuvent comporter des lettres. En binaire, un digit est également
appelé "bit", en abréviation de "BInary digiT".
Lorsque nous parlerons de, ou des, digit(s) de poids faible, il s'agira
de ceux correspondant à la partie droite d'une écriture,
en comptant de droite à gauche, et quand nous parlerons de digits
de poids fort, il s'agira de ceux de gauche du nombre. Par exemple, dans
le nombre 0b1001010, le bit de poids fort vaut 1, et les quatre bits de
poids faible valent 0b1010.
II:\ Passage d'une base à une autre
Savoir différencier une base d'une autre est certes utile, mais
il peut être quasiment indispensable de passer de l'une à
l'autre.
Certains d'entre-vous ont peut-être déjà étudié
ceci (Voila quelques années, c'était au programme de Spécialité
Maths, en Terminale S, je ne sais pas si c'est toujours le cas : les programmes
de Lycée ont changé depuis). Si vous êtes dans ce
cas, vous pouvez passer à la partie suivante (une fois n'est pas
coutume), bien qu'un petit rappel ne fasse jamais de mal...
Tout d'abord, voici un petit tableau de correspondance :
| Décimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Binaire | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| Hexadécimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
A: De décimal vers binaire et hexadécimal
Que l'on veuille passer de décimal vers binaire, ou de décimal vers hexadécimal, le raisonnement est fondamentalement le même. Nous noterons ici b la base de destination, que ce soit binaire, ou hexadécimal.
La méthode que je considère comme la plus simple est celle-ci :
- On divise le nombre en base 10 par b.
=> On obtient un quotient q1. - On divise q1 par b.
=> On obtient un quotient q2. - On divise q2 par b.
=> On obtient un quotient q3. - Et ainsi de suite...
- Quand le quotient obtenu vaut 0, on cesse les divisions, et on "remonte" dans la liste des restes obtenus, en les écrivant de gauche à droite.
Par exemple, on veut convertir 167 de la base 10 vers la base 2 :
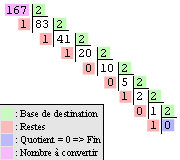
Donc, on a : 167 = 0b10100111.
Convertissons à présent 689 de la base 10 vers la base
16 (L'organisation de la succession de divisions est la même que
pour le premier exemple) :
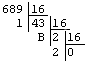
Donc, on a : 689 = 0x2B1.
B: De binaire et hexadécimal vers décimal
Peu importe la base source, si la base de destination est le décimal,
on procède toujours de la même façon. Nos noterons
ici b la base d'origine, que ce soit le binaire, ou l'hexadécimal.
La méthode, bien que extrêmement simple est assez difficile
à expliquer. En supposant que l'on ai un nombre xyzt en base b,
voici comment procéder :
xyzt = x*b^3 + y*b^2 + z*b^1 + t*b^0
Et ensuite, on calcule le membre de droite de cette expression.
Je pense que deux exemples suffiront à clarifier mes dires :
Par exemple, convertissons 0x11010010 en décimal :
0x11010010 = 1*2^7 +
1*2^6 + 0*2^5 + 1*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 0*2^0
= 1*128 +
1*64 + 0*32 + 1*16 + 0*8 + 1*4 + 1*2 + 0*1
= 422
Donc, 0x11010010 = 422.
A présent, convertissons 0x5DA1 en décimal :
0x5DA1 = 5*16^3 + D*16^2
+ A*16^1 + 1*16^0
= 5*4096 + 13*256 + 10*16 + 1*1
= 23969
Donc, 0x5DA1 = 23969.
C: De binaire à hexadécimal, et inversement :
Il n'y a rien de plus facile : il suffit de se rappeler qu'un digit hexadécimal correspond à quatre digits binaires, et que la conversion se fait du quartet (groupe de quatre bits, parfois aussi appelé "Nibble") de poids faible vers celui de poids fort, en remplissant éventuellement de 0 à gauche si nécessaire. Il suffit ensuite d'utiliser le tableau de correspondance donné plus haut.
Par exemple, convertissons 0b101100100110101010 en hexadécimal
:
0b10.1100.1001.1010.1010
= 0b0010.1100.1001.1010.1010
= 0x 2 C 9
A A
Donc, 0b101100100110101010 = 0x2C9AA.
Et convertissons 0x1B2D en binaire :
0x1B2D = 0b0001.1011.0010.1101
= 0b1101100101101
Donc, 0x1B2D = 0b1101100101101.
Voila la fin de cette première annexe atteinte.
Notez que votre TI-89/92/V-200 est parfaitement capable de réaliser
les conversions de base entre binaire, décimal, et hexadécimal...
mais reconnaissez qu'il peut être intéressant de parvenir
à se passer de la calculatrice !